|
Ja, ja, das Drehmoment. Jeder hat es (irgendwo in den Tiefen des Motors, man kommt da sehr schlecht ran), aber wer weiss schon, was ein Drehmoment so macht den ganzen Tag, wozu das gut ist oder auch nicht, und warum alle immer nur über PS reden? Im Internet gib es wahrscheinlich mindestens drölf Erklärungsversuche zu dem Thema "Auto und Drehmoment", aber einen guten habe ich dabei noch nicht gefunden. Schon manch einer hat sich eine Menge Mühe gemacht, das Thema allgemeinverständlich darzustellen, aber trotz teilweise guter Ansätze kommt dann häufig so viel Blödsinn dabei raus, dass ich mich genötigt sehe, jetzt endlich einmal die drölfundeinte Version zu dem Thema aufzulegen. Dabei werde ich versuchen, auf komplizierte Formeln zu verzichten und so viel wie möglich im Klartext zu formulieren. Und wer jetzt meint, ich würde hier ebenfalls eine Menge Unsinn verzapfen, der schreibt mir einfach eine Mail an [email protected], und wir diskutieren das aus. Über Feedback und Ergänzungen freue ich mich immer... :-) Grundlagen Wer in Physik aufgepasst hat, kann dieses Kapitel überspringen. Aber wer in Physik aufgepasst hat, weiss ohnehin, was ein Drehmoment ist, und braucht diesen Artikel an sich einfach nicht! :-) Kommen wir zum Thema... Also, es heiss "das" Drehmoment und hat mit "dem" Moment der Zeitrechnung überhaupt nichts zu tun. Ganz simpel ausgedrückt ist ein Drehmoment eine Kraft im Kreis herum. Aber was ist eine Kraft? Auch das lässt sich nicht in zwei Sätzen erklären, aber ich gehe davon aus, dass auch diejenigen Leser, die nicht (oder nicht so ganz genau) wissen (oder es in der Schule mal wussten und es nach der Klassenarbeit dann vergessen haben, weil sie es hinterher nie wieder gebraucht haben), was ein Drehmoment ist, eine gewisse Vorstellung davon haben, was eine Kraft ist. Wenn ich also eine 1kg schwere Kugel in einer (gewichtslosen) Tüte festhalte, dann übe ich auf die Kugel eine Kraft aus (und sie auf mich). Wenn auf die Kugel eine Kraft wirkt, warum bewegt sie sich dann nicht? Nun, es gibt da noch eine zweite Kraft, die Schwerkraft, welche sich aus der Erdbeschleunigung (1 g = 9,81 m/s²) und der Masse der Kugel ergibt. Die beiden Kräfte sind gleich gross und wirken entgegengesetzt, deswegen heben sie sich auf, und darum bewegt sich die Kugel nicht. Was lernen wir daraus? Kräfte sind gerichtete (vektorielle) Grössen, sie haben einen Betrag und eine Richtung. Kraft ist definiert als das Produkt aus Masse und Beschleunigung (F=m*a), wobei Beschleunigung definiert ist als Änderung der Geschwindigkeit pro Zeit. Die physikalische Einheit für die Kraft heisst Newton (N), 1 N = 1 kg * m/s². Eine Masse von 1 kg hat demnach eine Gewichtskraft von 1 kg * 9,81 m/s² = 9,81 N. Auf dem Mond hat eine Masse von 1 kg immer noch eine Masse von 1kg (logisch), aber die Gewichtskraft ist sehr viel niedriger. Ok, jetzt weiss wieder jeder, was eine Kraft ist, und wenn gleich der Begriff Newton auftaucht, dann ist auch keiner überfordert. Weiter: Arbeit ist das Produkt aus Kraft und Weg (W=F*s), wer über eine Strecke von 1m eine Kraft von 1N aufbringt, der hat eine Arbeit von 1Nm (Newtonmeter) erbracht. Hier darf man sich nicht verwirren lassen, die physikalische Einheit für Arbeit, Energie und Drehmoment ist kg*m²/s². Um die Missverständnisse zu minimieren, benutzt man für Energie die Einheit J (Joule), für Arbeit Ws (Wattsekunde) und für Drehmoment Nm (Newtonmeter). Aber es gilt 1 kg * m² / s² = 1 J = 1 Nm = 1 Ws. Jetzt kennen wir Kraft und Arbeit, doch was ist Leistung? Leistung ist Arbeit pro Zeit (P = W/t). Die Einheit der Leistung ist W (Watt). 1W = 1kg*m²/s³. Wer in einer Sekunde die Arbeit von 1Ws erledigt, der hat in dieser Sekunde mit einer Leistung von 1 Watt gearbeitet. Das Drehmoment als solches bei coolen und uncoolen Drehbewegungen Jetzt stellen wir uns mal eine Mauer mit Loch vor, und dadurch stecken wir jetzt eine Achse. An der einen Seite befestigen wir einen grossen Schleifstein, und an der anderen eine Kurbel. Die Achse sei optimal gelagert, es gibt auch sonst keine Reibung. Und jetzt schauen wir mal in das Physikbuch. Da steht: Unter einem Drehmoment versteht man das Produkt aus einer Kraft und dem senkrechten Abstand ihrer Wirkungslinie vom Drehpunkt. Stellen wir uns mal vor, die Kurbel stehe waagerecht, und wir hängen jetzt ans Ende der Kurbel ein Gewicht von etwas über einem Kilogramm mit einer Gewichtskraft von 10 N. Das ist also unsere Kraft. Da diese Kraft nach unten gerichtet ist, wirkt sie genau senkrecht zur Kurbel. Die Kurbellänge ist der "senkrechte Abstand" aus der Definition von oben. Der Drehpunkt ist in diesem Fall die Achse. Die Kurbel sei mal genau 10cm lang. Dann wirkt auf die Achse ein Drehmoment von 10N*0,1m = 1Nm. Auf der anderen Seite ist immer noch der Schleifstein. Dieser Stein hat ein (Massen-)Trägheitsmoment. Oh, nein! Schon wieder ein Moment, das wird ja immer schlimmer... Und das will ich jetzt auch gar nicht weiter vertiefen, aber ein Trägheitsmoment ist halt das Äquivalent zur Masse, wenn man die Drehbewegung mit der "normalen" Geradeausbewegung vergleicht. Das Physikbuch sagt: Unter der Wirkung eines Drehmomentes erfährt ein drehbarer starrer Körper eine Winkelbeschleunigung (=Äquivalent zur "normalen Geradeausbeschleunigung"). So, und dann fängt der Schleifstein an, sich zu drehen. Und damit ändert sich der wirksame Hebelarm, weil sich die Kurbel mitdreht, das Gewicht aber weiterhin nach unten zieht. Das Ganze wird also endlos hin und her pendeln (wir hatten ja die Reibung ausgeschaltet, die bewirkt hätte, dass das ganze irgendwann mal mit hängender Kurbel zum Stehen kommt). Das war also ganz sicher keine coole Drehbewegung. Jetzt machen wir das ganze nochmal richtig! Statt eines Gewichtes an der Kurbel krempeln wir die Ärmel hoch und drehen selbst an der Kurbel, und zwar mit konstant 10 N (eine Hausfrau hat das im Gefühl) und immer senkrecht zur Kurbel. Und so bekommen wir eine richtig schöne Drehbewegung. Die wird immer schneller und schneller und schneller... Bis sie unendlich schnell ist oder uns die Schulter auskugelt. Das war fast eine coole Drehbewegung, aber noch nicht ganz. Wir schalten die Reibung wieder ein. Willkommen in der realen Welt. Reibung ist toll, sie verhindert unendlich schnelle Drehbewegungen. Es gibt Reibungskräfte, die sind proportional zur Geschwindigkeit (doppelte Geschwindigkeit erzeugt doppelte Reibung), andere wachsen quadratisch (doppelte Geschwindigkeit erzeugt vierfache Reibung) oder noch schlimmer. So lange die Antriebskraft (oder das Antriebsmoment) grösser als die Reibungskraft (oder das Reibungsmoment ist), wirds immer schneller. Wenn sich die Geschwindigkeit nicht verändert, dann halten sich Antriebs- und Bremskräfte die Waage (und löschen sich gegenseitig aus), das gilt sogar für den Stillstand (keine Antriebskraft, keine Geschwindigkeit also auch keine Reibung). Jetzt kurbeln wir also nochmal mit 10 N an der Zehnzentimeterkurbel herum und erzeugen wieder dauerhaft ein Drehmoment von 1 Nm, der Schleifstein dreht sich immer schneller, und zwar so lange, bis sich das entgegenwirkende Reibungsmoment ebenfalls auf 1 Nm eingestellt hat. Dann dreht sich der Schleifstein mit - sagen wir mal - einer Umdrehung pro Sekunde. Die Leistung, die wir erbringen, errechnet sich nach der Formel also 2 * 3,14 * 1Nm * 1/s und ist demnach 6,28 Watt. Merke: Die Leistung ist proportional zum Produkt aus Drehmoment und Drehzahl. Wer das einmal verinnerlicht hat, ist eigentlich schon am Ziel, denn daraus lässt sich so ziemlich jeder Zusammenhang ableiten. Drehmoment und Autos Autos müssen viel PS haben. Das meinen zumindest die meisten Autofahrer, ich hab auf jeden Fall noch keinen getroffen, der über zuviel Leistung geklagt hat. Aber was ist denn ein PS? PS ist eine Einheit für Leistung, allerdings nicht die offizielle, die ist nämlich Watt (W). Auch schon mal gehört, oder? 1 W = 0,00136 PS, bzw. 1 kW = 1,36 PS. Und da Leistung, Drehzahl und Drehmoment über die oben genannte Formel unweigerlich miteinander verknüpft sind, kann also bei gegebener Drehzahl und bekanntem Drehmoment die abgegebene Leistung berechnet werden. Solche Werte werden auch in Diagrammen dargestellt (z.B. Drehmoment über Drehzahl), sie sind motorspezifisch und erlauben schon auf den ersten Blick eine Aussage über die Motorcharakteristik, dazu später mehr. Hier mal ein Beispiel: 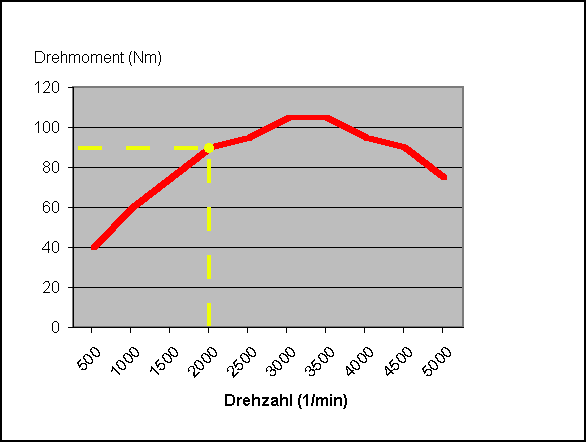 Abb. 1: Drehmomentverlauf eines Motors über der Drehzahl Gegeben ist also der Verlauf des Drehmoments eines beliebigen Motors über seiner Drehzahl. Berechnen wir mal die Leistung für eine bestimmte Drehzahl (gelbe Markierung): Drehzahl n = 2000 1/min = 33,3 1/s Drehmoment M = 90 Nm Leistung P = 2 * Pi * M * n = 2 * 3,14 * 90Nm * 33,3 1/s = 18,8 kW Bei 2000 Umdrehungen pro Minute leistet diese Maschine also 18,8 Kilowatt. Das lässt sich ebenfalls mit in das Diagramm einzeichnen, und zwar für alle Drehzahlen:  Abb. 2: Drehmoment- und Leistungsverlauf eines Motors über der Drehzahl Die maximale Leistung hat der Motor also bei ca. 4500 Touren, während das maximale Drehmoment schon bei ca. 3000 Touren anliegt. Bei Höchstdrehzahl (5000 Touren) hat er also weder maximale Leistung noch maximales Drehmoment. Warum also macht es unter Umständen trotzdem Sinn, für die maximale Beschleunigung einen Gang bis an die Drehzahlgrenze auszufahren? Das klären wir später... Diese Maschine bauen wir jetzt in ein Auto und fahren damit 50 km/h bei 2000 U/min. Die Summe aus allen Reibungen (Luftwiderstand, mechanische Reibung im Motor, in den Reifen,...) ergebe sich zu einem Äquivalent von 8 kW, der Motor muss also 8 kW leisten, damit der Wagen nicht schneller oder langsamer wird. Wie wir oben berechnet haben, beträgt die Motorleistung aber 18,8 kW, der Wagen müsste also beschleunigen, oder? Warum tut er das nicht? Ganz einfach: Bei der in Abb. 1 gezeigten Kurve handelt es sich um die Vollastkurve, d.h. die Maximalwerte zu jeder Drehzahl. Wollte man alle möglichen Betriebszustände (also auch Teillast und Schiebebetrieb) darstellen, dann sähe das Diagramm so aus, wäre aber nicht übersichtlicher: 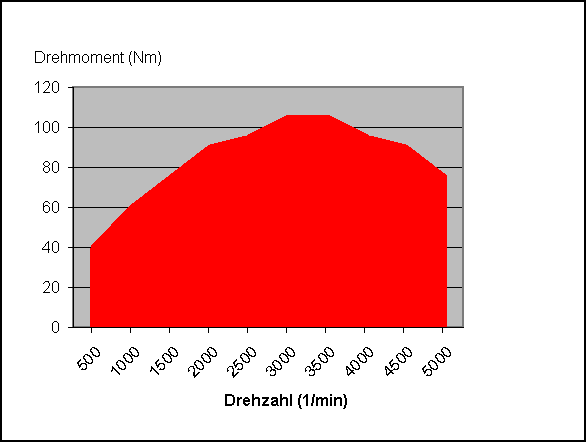 Abb. 3 Darstellung Drehmoment über der Drehzahl aller Betriebszustände eines Motors mit einem Drehmoment >=0 Nm Genau genommen gibt es sogar auch negative Drehmomente, wenn der Motor z.B. im Schiebebetrieb mit Spritabschaltung als Bremse fungiert, aber die sind hier nicht dargestellt. Worauf ich eigentlich hinaus wollte: Drehmomentkurven von Verbrennungsmotoren sind immer (also wenn nicht explizit etwas anderes dabei steht) Vollastkurven. Der Motor aus dem Beispiel kann also bei einer Drehzahl von 2000 1/min maximal 90 Nm Drehmoment produzieren und somit maximal 18,8 kW leisten, aber eben nur unter Vollast, er kann auch im Teillastbereich genau 8 kW leisten. So, jetzt nähern wir uns mal des Pudels Kern: Was trägt denn nun das Drehmoment zur Beschleunigung eines Fahrzeuges bei? Der Einfachheit halber gehen wir mal von zwei identischen Fahrzeugen aus, die genau 60 km/h fahren. Beide haben oben genannten Motor eingebaut. Das eine fährt im vierten Gang mit 3000 1/min, das andere im dritten Gang mit 4000 1/min. Beide geben gleichzeitig Vollgas, welches hat die Nase vorn? Was ist ausschlaggebend: Mehr Drehzahl, mehr Drehmoment oder mehr Leistung? (...) (Zeit für eine kurze Denkpause) Natürlich hat der die Nase vorn, der im dritten Gang unterwegs ist, das lässt sich schon aus dem Gefühl heraus sagen, aber wie lässt sich das physikalisch untermauern? Betrachten wir mal die Drehmomente, die Motorleistung und die Übersetzung:
(* Für Fahrzeug A willkürich gewählt, für B berechnet: Ü = 3000 / 4000 * 1 = 0,75) Es beschleunigt also der besser, dessen Motor mehr Leistung abgibt, es kommt nur auf die Leistung an, sonst auf gar nichts! Wozu dann das ganze Herumgerechne mit dem Getriebe? Was macht eigentlich ein Getriebe? Mit einem Transformator kann ich eine Kombination aus Spannung und Strom umwandeln in eine andere Kombination aus Spannung und Strom, aber die Leistung, das Produkt aus Strom und Spannung, ist auf beiden Seiten identisch (Verluste vernachlässigt). Genau so funktioniert auch ein Getriebe, auf der einen Seite kommt eine Kombination aus Drehmoment und Drehzahl rein, und auf der anderen Seite eine andere wieder heraus, die Leistung ist aber auf beiden Seiten identisch (Verluste vernachlässigt). Das Getriebe ermöglicht es somit, immer in einem Drehzahlbereich zu fahren, der dem Motor "liegt". Was bedeutet das jetzt für die Schaltzeitpunkte? Für maximale Beschleunigung ist dann zu schalten, wenn der Motor bei der Drehzahl, die er nach dem Schalten haben wird, eine höhere Leistung abgeben kann, als bei der, die er gerade hat. Damit ist dann auch das Drehmoment, das am Reifen ankommt, grösser, da sich ja die Reifendrehzahl durchs Schalten nicht ändert. Weil die meisten Automotoren ihre maximale Leistung kurz vor dem Drehzahlmaximum haben, macht es auch Sinn, für grösstmögliche Beschleunigung die Gänge bis ans Limit auszufahren, denn in einem höheren Gang ist die Leistung des Motors meist schon wieder deutlich geringer. Wer es genau wissen will, muss halt rechnen. Dazu braucht man die Übersetzung eines jeden Ganges und ein genaues Leistungs-Drehzahl-Diagramm, dann kann man für jeden Gangwechsel die ideale Drehzahl ausrechnen. Charakterisierung eines Motors Die blosse Angabe der Leistung eines Motors ist ebenso wenig aussagekräftig wie die Angabe des maximalen Drehmomentes. Um genau zu verstehen, wie sich ein Motor verhält, ist das Drehmoment-Drehzahl- oder das Leistungs-Drehzahl-Diagramm essentiell. Schliesslich verhalten sich unterschiedliche Motorentypen trotz evtl. gleicher Maximalleistung ganz anders, der Unterschied zwischen Gleichstrom- und Verbrennungsmotoren beispielsweise ist gravierend. Da aber die meisten Fahrzeuge mit Verbrennungsmotoren ausgerüstet sind, kann man anhand der Angabe "Turbodiesel mit 120 PS" oder "Benziner mit 125 PS" schon Einiges über deren Verhalten ableiten. Manche Motoren werden als "drehfaul", andere als "elastisch", "dieseltypisch" oder "turbotypisch" bezeichnet. Was bedeutet das für ihre Drehmoment- und Leistungskurven? Kann man dieses Verhalten anhand der Kurven ablesen? Antwort: Ganz klar ja! Hier einmal einige Beispiele, bei denen es nur um die qualitative Darstellung geht, deswegen ohne Skalierung: 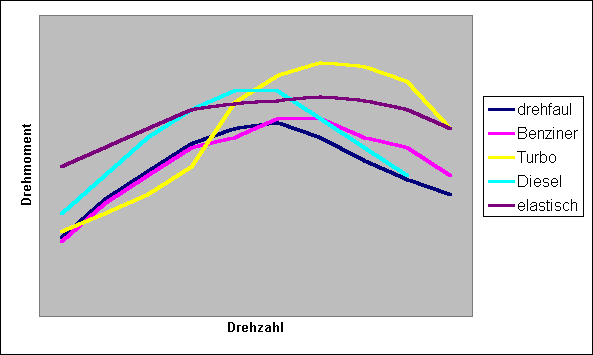 Abb. 4 Qualitative Darstellung einiger typischer Drehmomentverläufe von Verbrennungsmotoren über der Drehzahl Den Verlauf des typischen Benziners haben wir schon kennengelernt. Wie unterscheidet sich der Drehmomentverlauf eines typischen Saugerdiesels mit annähernd gleicher Maximalleistung? Nun, im unteren Drehzahlbereich verfügt der Diesel über mehr Drehmoment und somit auch mehr Leistung, aber er erreicht sein Drehmomentmaximum eher und dreht insgesamt auch nicht so hoch. Deswegen liegt die Leistungskurve des Benziners im oberen Bereich über der des Diesels (siehe Abb. 5). 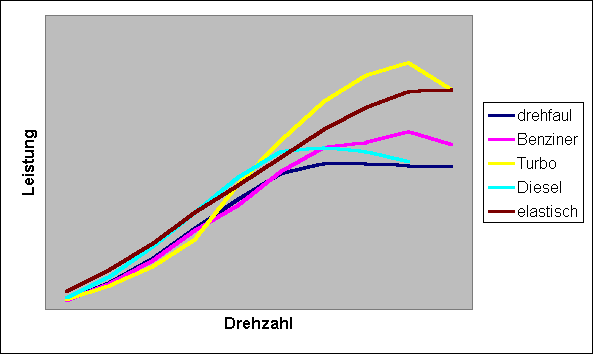 Abb. 5 Qualitative Darstellung einiger typischer Leistungsverläufe von Verbrennungsmotoren über der Drehzahl (passend zu Abb. 4) Typisch für Turbomotoren ist das sogenannte "Turboloch", eine massive Schwäche im unteren Drehzahlbereich. Beschleunigt man von unten heraus, passiert zunächst lange Zeit wenig, aber dann setzt die Leistung schlagartig ein. Der Motor ist dadurch unelastisch und nur in einem schmalen Drehzahlband nutzbar, dafür lässt sich aus dem vorhandenen Hubraum eine relativ hohe Maximalleistung herausholen. Moderne Turbomotoren haben kaum noch solch massive Knicks in den Kurven (z.B. durch variable Schaufelgeometrie im Lader), aber prinzipiell verhalten sich aufgeladene Motoren (das gilt weitestgehend auch für Kompressoren und G-Lader) mehr oder weniger wie hier dargestellt. Ein Motor wirkt drehfaul, wenn man das Gefühl hat, dass im oberen Drehzahlbereich automatisch die Handbremse angezogen wird. Trotz hoher Drehzahlen geht es irgendwie nicht so richtig ab, die Maschine wirkt angestrengt. Das liegt daran, dass nach Erreichen des maximalen Drehmomentes die Kurve übermässig stark abfällt, was sich auch in der Leistungskurve durch ein Plateau (oder schlimmer noch: Durch Abfallen der Leistungskurve) zeigt. Solche Motoren machen prinzipiell eher wenig Spass. Ganz anders hingegen elastische Maschinen, die sich durch gleichmässige Leistungsentfaltung auszeichnen und schon kurz über Leerlauf kräftig zupacken, also bereits früh ein grosses Drehmoment und damit eine hohe Leistung entwickeln. Sie ermöglichen schaltfaules und souveränes Fahren. Auch aus niedrigen Drehzahlen beschleunigen sie kräftig, ohne dabei angestrengt zu wirken. Dies ist die Charakteristik von grossvolumigen Acht- und Zwölfzylindern. Prinzipiell gilt: - Je mehr Hubraum desto mehr Drehmoment und Leistung. - Turbolader, Kompressoren und G-Lader erhöhen die spezifische Leistung (Maximal-Leistung pro Hubraum, angegeben z.B. in PS/Liter) sowie den Verbrauch. - Je mehr Zylinder, desto elastischer die Leistungsentwicklung, desto geringer die Maximaldrehzahl. - Saugdiesel haben ein höheres maximales Drehmoment und eine geringere maximale Leistung als Saugbenziner gleichen Hubraumes. Ausserdem drehen sie nicht so hoch. - Die Beschleunigung eines Fahrzeuges hängt von "unendlich" vielen Faktoren ab, die wichtigsten sind: Leistungskurve des Motors, Gewicht, Geschwindigkeit bzw. Luftwiderstand und sonstige Reibungskräfte, Getriebe und Fahrer. - Ausnahmen bestätigen die Regel. Test An dieser Stelle möchte ich den grossen Philosophen H. Schneider zitieren: "Hefte raus! Klassenarbeit!". Wer will, kann sich hier ja noch einmal selbstkritisch überprüfen. Einige Fragen sind ganz simpel, andere bewusst "fies" gestellt, also genau durchlesen. Auflösungen gibts unten. 1) Richtig oder falsch? Die Einheit von PS lautet Nm/s. 2) Richtig oder falsch? Leistung ist die Dauer der Arbeit. 3) Richtig oder falsch? 1 kW = 1,36 PS 4) Richtig oder falsch? Für optimale Beschleunigung muss dann geschaltet werden, wenn der Motor im nächsthöheren Gang mehr Drehmoment zur Verfügung stellt als im derzeitigen. 5) Richtig oder falsch? Bei gegebener Drehzahl und bekanntem Drehmoment lässt sich die abgegebene Leistung berechnen. 6) Richtig oder falsch? Drehmoment und Leistung stehen in keinem direkten Zusammenhang. 7) Was muss erhöht werden, um die Endgeschwindigkeit zu steigern: Die maximale Leistung oder das maximale Drehmoment? 8) Richtig oder falsch? Aus einem Drehmoment-Drehzahl-Diagramm kann für eine gegebene Drehzahl eindeutig das zugehörige Drehmoment abgelesen werden. 9) Richtig oder falsch? Aus einem Drehmoment-Drehzahl-Diagramm kann für ein gegebenes Drehmoment eindeutig die zugehörige Drehzahl abgelesen werden. 10) Richtig oder falsch? Aus einem Drehmoment-Drehzahl-Diagramm kann für eine gegebene Drehzahl die zugehörige Maximalleistung eindeutig abgelesen werden. 11) Richtig oder falsch? Die Informationen aus einem Drehmoment-Drehzahl-Diagramm sind ausreichend, um die Maximalleistung des Motors zu berechnen. 12) Richtig oder falsch? Die grösste Beschleunigung erfährt man auf dem Drehmomentgipfel des Motors. Bei höherer oder niedrigerer Drehzahl ist die Beschleunigung nicht so gross. 13) Richtig oder falsch? Beim Beschleunigen spürt man die "Newtonmeter", nicht die "PS". 14) Richtig oder falsch? Die Leistung eines Motors kann prinzipiell nicht "zu hoch" sein. Antworten 1) Falsch! PS ist ebenso wie kW oder Nm/s eine Einheit für eine Leistung. Die offizielle Einheit ist Watt, ein Watt ist 1 kg * m²/s³ bzw. 1 Nm/s. 2) Falsch! Leistung ist Arbeit pro Zeit (P = W / t). Die Dauer der Arbeit ist einfach die Arbeitsdauer, also eine Zeit. 3) Richtig! 4) Falsch! Es muss dann geschaltet werden, wenn der Motor im nächsthöheren Gang mehr Leistung (!) zur Verfügung stellt als im derzeitigen. Unter Umständen hat er dann auch mehr Drehmoment, aber das ist nicht das Kriterium. 5) Richtig! Die Leistung P (in Watt) berechnet sich aus der Drehzahl n (in Umdrehungen pro Sekunde) und dem Drehmoment M (in Newtonmetern). P = 2 * Pi * M * n 6) Falsch! Siehe obige Formel, Drehmoment und Leistung sind über die Drehzahl eindeutig miteinander verknüpft. 7) Die maximale Leistung. 8) Falsch! Es kann das zugehörige maximale (!) Drehmoment abgelesen werden, aber ein Motor kann bei einer bestimmten Drehzahl prinzipiell jedes Drehmoment zwischen 0 Nm und dem Maximalwert abgeben, ggf. sogar negative Werte (als Motorbremse). 9) Falsch! Es gibt prinzipiell "unendlich" viele Drehzahlen, an denen er ein bestimmtes Drehmoment abgeben kann. Ausnahmen: 1) Das gegebene Drehmoment befindet sich ausserhalb der Möglichkeiten dieses Motors. 2) Das gegebene Drehmoment ist genau der Wert des Maximal-Drehmomentes. Beispiel: Unser bekannter Benzinmotor hat sowohl bei 2000 1/min als auch bei 4500 1/min ein maximales Drehmoment von 90 Nm, aber natürlich kann er auch bei jeder Drehzahl dazwischen genau 90 Nm abgeben. Die "unendlich" vielen Betriebszustände befinden sich also alle auf der Linie zwischen den beiden genannten Punkten. 10) Falsch! Es kann das zugehörige maximale Drehmoment (!) abgelesen werden, die zugehörige Maximalleistung für diese Drehzahl kann aber berechnet werden. 11) Richtig! Allerdings kann die zur Maximalleistung gehörige Drehzahl nicht einfach abgelesen werden, da sie für gewöhnlich weder der Maximaldrehzahl noch der Drehzahl des maximalen Drehmomentes entspricht. Bei Verbrennungsmotoren liegt dieser Punkt bei ca. (!!!) 90% der Maximaldrehzahl, d.h. in diesem Bereich sollten mal ein paar Stichproben durchgeführt werden. 12) Falsch! Maximale Beschleunigung gibt's bei maximaler Leistung, das ist in der Regel nicht gleichzeitig der Drehmomentgipfel. 13) Falsch! Für die Beschleunigung ist die Leistung verantwortlich, dabei ist es unerheblich, ob die sich aus einem grossen Drehmoment bei kleiner Drehzahl oder kleinem Drehmoment bei grosser Drehzahl ergibt. 14) Richtig! Mehr Leistung ist immer besser, und noch mehr Leistung ist immer noch besser... :-) 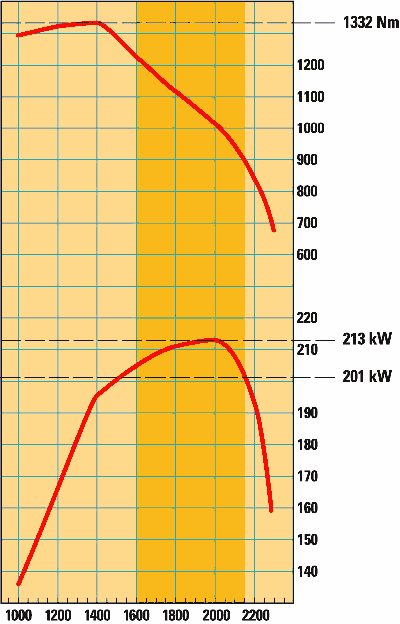 Abb. 6 Drehmoment-Leistungs-Drehzahl-Diagramm eines LKW-Diesels Dies ist das Diagramm eines Dieselmotors für Baumaschinen, der ein gesundes Drehmoment von über 1300 Nm bereits bei 1400 1/min erreicht. Trotzdem liegt die Maximalleistung nur bei 213 kW (deutlich unter 300 PS), weil die Drehmomentkurve danach dieseltypisch stark abfällt. Dafür leistet er aber bereits bei etwas über 1000 1/min 140kw (knapp 200 PS), und das macht ihm so schnell kein PKW-Motor nach... 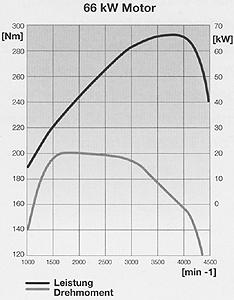 Abb. 7 Drehmoment-Leistungs-Drehzahl-Diagramm eines Wohnmobil-Diesels Das ist das Diagramm eines Dieselmotors für Wohnmobile. Er leistet maximal 66 kW (90 PS), erreicht das maximale Drehmoment aber auch schon früh bei ca. 1500 1/min. 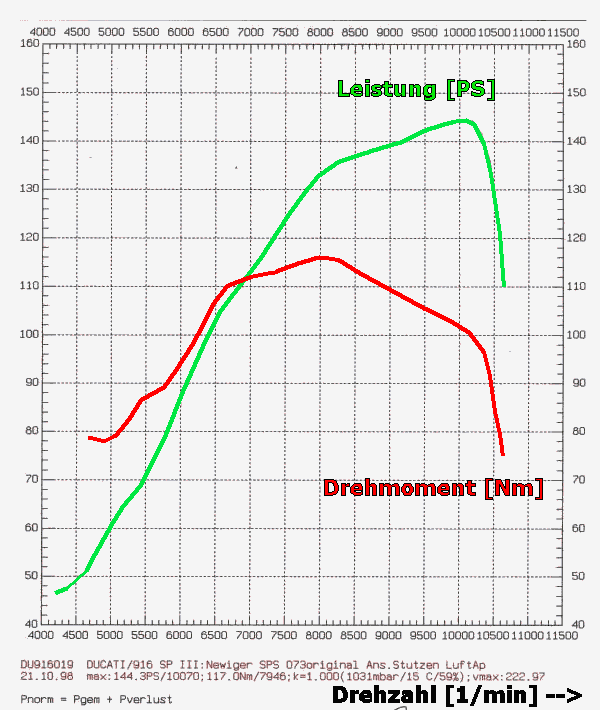 Abb. 8 Leistungs-Drehmoment-Drehzahl-Diagramm eines Motorradmotors Dies ist das andere Extrem zum Baumaschinendiesel: Ein Motorradmotor. Er dreht sehr hoch (10600 1/min) und hat ein vergleichsweise verschwindend geringes maximales Drehmoment (117 Nm bei ca. 8000 1/min), die Maximalleistung ist mit 106 kW (144 PS) bei ca. 10000 1/min aber recht ordentlich, für ein Motorrad allemal... 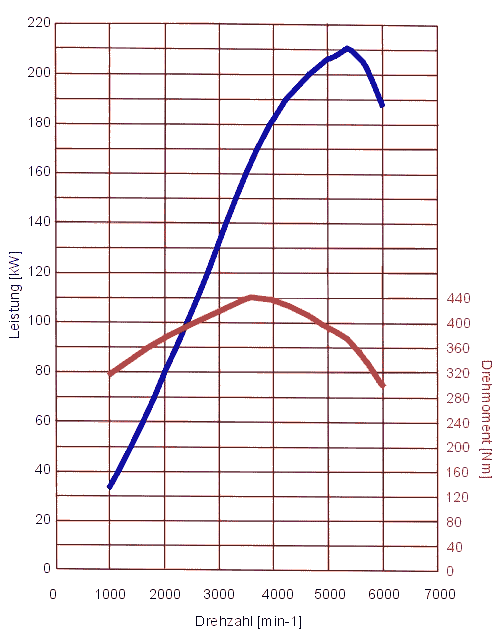 Abb. 9 Leistungs-Drehmoment-Drehzahl-Diagramm des 540i E39 Schön zu sehen hier ist der flache Verlauf der Drehmomentkurve des 4,4-Liter-V8, der die Leistungskurve fast wie mit dem Lineal gezogen ansteigen lässt. Diese Maschine verspricht Fahrspass pur, denn sie ist drehfreudig und bärenstark. Im Drehzahlbereich von 1500 bis 5600 Touren stehen mindestens 80% des maximalen Drehmomentes zur Verfügung - schaltfaules Fahren ist problemlos möglich. Nachwort So, das war's. Eigentlich gar nicht so kompliziert, oder? Gerne wäre ich noch tiefer in die Physik eingestiegen, aber dies soll ja keine Doktorarbeit werden und auch kein Studium ersetzen. Ich hoffe, das Lesen hat genau so viel Spass gemacht wie das Schreiben! Wer noch Fragen hat oder mich auf Fehler oder missverständliche Formulierungen aufmerksam machen möchte, der sollte das unbedingt tun! www.rieseler-online.de |